Refreshing memory... diffuse light (red book)
RGB Values for Lights and Materials
The color components specified for lights mean something different than for materials. For a light, the numbers correspond to a percentage of full intensity for each color. If the R, G, and B values for a light's color are all 1.0, the light is the brightest possible white. If the values are 0.5, the color is still white, but only at half intensity, so it appears gray. If R=G=1 and B=0 (full red and green with no blue), the light appears yellow.
For materials, the numbers correspond to the reflected proportions of those colors. So if R=1, G=0.5, and B=0 for a material, that material reflects all the incoming red light, half the incoming green, and none of the incoming blue light. In other words, if an OpenGL light has components (LR, LG, LB), and a material has corresponding components (MR, MG, MB), then, ignoring all other reflectivity effects, the light that arrives at the eye is given by (LR*MR, LG*MG, LB*MB).
Similarly, if you have two lights that send (R1, G1, B1) and (R2, G2, B2) to the eye, OpenGL adds the components, giving (R1+R2, G1+G2, B1+B2). If any of the sums are greater than 1 (corresponding to a color brighter than the equipment can display), the component is clamped to 1.
The ultimate diffuse light equation..
(max { L · n , 0} ) * diffuselight * diffusematerial
Where L = Normalised vector from vertex to light source.
n = Normal of the polygon at the vertex.
OR
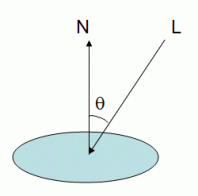
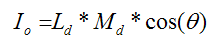
where I is the reflected intensity, Ld is the light's diffuse color (gl_LightSource[0].diffuse), and Md is the material's diffuse coefficient (gl_FrontMaterial.diffuse).
The color components specified for lights mean something different than for materials. For a light, the numbers correspond to a percentage of full intensity for each color. If the R, G, and B values for a light's color are all 1.0, the light is the brightest possible white. If the values are 0.5, the color is still white, but only at half intensity, so it appears gray. If R=G=1 and B=0 (full red and green with no blue), the light appears yellow.
For materials, the numbers correspond to the reflected proportions of those colors. So if R=1, G=0.5, and B=0 for a material, that material reflects all the incoming red light, half the incoming green, and none of the incoming blue light. In other words, if an OpenGL light has components (LR, LG, LB), and a material has corresponding components (MR, MG, MB), then, ignoring all other reflectivity effects, the light that arrives at the eye is given by (LR*MR, LG*MG, LB*MB).
Similarly, if you have two lights that send (R1, G1, B1) and (R2, G2, B2) to the eye, OpenGL adds the components, giving (R1+R2, G1+G2, B1+B2). If any of the sums are greater than 1 (corresponding to a color brighter than the equipment can display), the component is clamped to 1.
The ultimate diffuse light equation..
(max { L · n , 0} ) * diffuselight * diffusematerial
Where L = Normalised vector from vertex to light source.
n = Normal of the polygon at the vertex.
OR

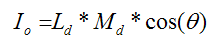
where I is the reflected intensity, Ld is the light's diffuse color (gl_LightSource[0].diffuse), and Md is the material's diffuse coefficient (gl_FrontMaterial.diffuse).


0 Comments:
Post a Comment
<< Home